Электростатическая энергия заряженного шара. Энергия электрического поля. (Примеры решения задач). §З.Электростатическая энергия ионного кристалла

Пример 2.

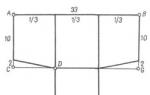
Определите электрическую энергию взаимодействия заряженного кольца с диполем, расположенным на его оси, как показано на рис.4. Известны расстояния a , l , заряды Q , q и радиус кольца R .

Решение .

При решении задачи следует учесть все энергии парных взаимодействий зарядов одного тела (кольца) с зарядами другого тела (диполя). Энергия взаимодействия точечного заряда q с зарядом Q , распределенным по кольцу, определяется суммой

где - заряд бесконечно малого фрагмента кольца, - расстояние от этого фрагмента до заряда q . Поскольку все одинаковы и равны , то

Аналогично найдем энергию взаимодействия точечного заряда –q с заряженным кольцом:

Суммируя W 1 и W 2 , получим для энергии взаимодействия кольца с диполем:

Электрическая энергия заряженных проводников

Пример 3.

Определите работу электрических сил при уменьшении в 2 раза радиуса однородно заряженной сферы. Заряд сферы q , ее первоначальный радиус R .

Решение .

Электрическая энергия уединенного проводника определяется формулой , где q – заряд проводника, j - его потенциал. Учитывая, что потенциал однородно заряженной сферы радиуса R равен , найдем ее электрическую энергию:

После уменьшения в два раза радиуса сферы ее энергия становится равной

Электрические силы при этом совершают работу

Пример 4.

Два металлических шара, радиусы которых r и 2r , а соответствующие заряды 2q и –q , расположены в вакууме на большом расстоянии друг от друга. Во сколько раз уменьшится электрическая энергия системы, если шары соединить тонкой проволокой?

Решение .

После соединения шаров тонкой проволокой их потенциалы становятся одинаковыми

а установившиеся заряды шаров Q 1 и Q 2 получаются в результате перетекания заряда с одного шара на другой. При этом суммарный заряд шаров остается постоянным:

Из этих уравнений найдем

Энергия шаров до соединения их проволокой равна

а после соединения

Подставляя в последнее выражение значения Q 1 и Q 2 , получим после простых преобразований

Пример 5.

В один шар слились N = 8 одинаковых шариков ртути, заряд каждого из которых q . Считая, что в начальном состоянии ртутные шарики находились на большом расстоянии друг от друга, определите, во сколько раз увеличилась электрическая энергия системы.

Решение .

При слиянии ртутных шариков сохраняется их суммарный заряд и объем:

где Q – заряд шара, R – его радиус, r – радиус каждого маленького ртутного шарика. Суммарная электрическая энергия N уединенных шариков равна

Электрическая энергия полученного в результате слияния шара

После алгебраических преобразований получим

= 4.

Пример 6.

Металлический шарик радиуса R = 1 мм и заряда q = 0,1 нКлс большого расстояния медленно приближают к незаряженному проводнику и останавливают, когда потенциал шарика становится равным j = 450 В. Какую работу для этого следует совершить?

Решение .

где q 1 и q 2 – заряды проводников, j 1 и j 2 – их потенциалы. Так как проводник по условию задачи не заряжен, то

где q 1 и j 1 заряд и потенциал шара. Когда шар и незаряженный проводник находятся на большом расстоянии друг от друга,

и электрическая энергия системы

В конечном состоянии системы, когда потенциал шара стал равным j, электрическая энергия системы:

Работа внешних сил равна приращению электрической энергии:

= –0,0225 мкДж.

Заметим, что электрическое поле в конечном состоянии системы создается зарядами, индуцированными на проводнике, а также зарядами, неоднородно распределенными по поверхности металлического шара. Рассчитать это поле при известной геометрии проводника и заданном положении металлического шара весьма непросто. Нам не потребовалось этого делать, поскольку в задаче задана не геометрическая конфигурация системы, а потенциал шара в конечном состоянии.

Пример 7.

Система состоит из двух концентрических тонких металлических оболочек с радиусами R 1 и R 2 ( и соответствующими зарядами q 1 и q 2 . Найдите электрическую энергию W системы. Рассмотрите также специальный случай, когда .

Решение .

Электрическая энергия системы из двух заряженных проводников определяется формулой

Для решения задачи необходимо найти потенциалы внутренней (j 1) и внешней (j 2) сфер. Это нетрудно сделать (см. соответствующий раздел пособия):

, .

Подставляя эти выражения в формулу для энергии, получим

При энергия равна

Собственная электрическая энергия и энергия взаимодействия

Пример 8.

Две проводящие сферы, заряды которых q и –q , радиусы R 1 и R 2 , расположены в вакууме на большом расстоянии друг от друга. Сфера большего радиуса R 2 состоит из двух полусфер. Полусферы разъединяют, подносят их к сфере радиуса R 1 , и вновь соединяют, образуя таким образом сферический конденсатор. Определите работу электрических сил при таком составлении конденсатора.

Решение .

Электрическая энергия двух удаленных друг от друга заряженных сфер равна

Электрическая энергия полученного сферического конденсатора:

Потенциал внутренней сферы, - потенциал внешней сферы. Следовательно,

Работа электрических сил при таком составлении конденсатора:

Заметим, что электрическая энергия сферического конденсатора W 2 равна работе внешних сил по зарядке конденсатора. При этом электрические силы совершают работу . Эта работа совершается не только при сближении заряженных обкладок, но и при нанесении заряда на каждую из обкладок. Поэтому A ЭЛ отличается от найденной выше работы A , совершенной электрическими силами только при сближения обкладок.

Пример 9.

Точечный заряд q = 1,5 мкКл расположен в центре сферической оболочки, по поверхности которой однородно распределен заряд Q = 5 мкКл. Найдите работу электрических сил при расширении оболочки – увеличении ее радиуса от R 1 = 50 мм до R 2 = 100 мм.

Решение .

Энергия взаимодействия точечного заряда q с зарядами, расположенными на сферической оболочке радиуса R равна

Собственная электрическая энергия оболочки (энергия взаимодействия зарядов оболочки между собой) равна:

Работа электрических сил при расширении оболочки:

После преобразований получим

1,8 Дж.

Другой способ решения

Точечный заряд представим в виде однородно заряженной сферы малого радиуса r и заряда q . Полная электрическая энергия системы равна

Потенциал сферы радиуса r ,

Потенциал сферы радиуса R . При расширении внешней сферы электрические силы совершают работу

После подстановок и преобразований получим ответ.

Пример 10.

Какая часть электрической энергии заряженного проводящего шара, расположенного в вакууме, заключена в пределах концентрической с шаром воображаемой сферы, радиус которой в n раз больше радиуса шара?

Решение .

Объемная плотность энергии электрического поля

определяет электрическую энергию , локализованную в бесконечно малом объеме (E – модуль вектора напряженности электрического поля в этом объеме, e - диэлектрическая проницаемость). Чтобы вычислить полную электрическую энергию заряженного проводящего шара, мысленно разобьем все пространство на бесконечно тонкие шаровые слои, концентрические с заряженным шаром. Рассмотрим один из таких слоев радиуса r и толщины dr (см. рис.5). Его объем равен

а сосредоточенная в слое электрическая энергия

Напряженность E поля заряженного проводящего шара зависит, как известно, от расстояния r до центра шара. Внутри шара , поэтому при вычислении энергии достаточно рассматривать только те шаровые слои, радиус r которых превышает радиус шара R .

При напряженность поля

диэлектрическая проницаемость и, следовательно

где q – заряд шара.

Полная электрическая энергия заряженного шара, определяется интегралом

а энергия, сосредоточенная внутри воображаемой сферы радиуса nR , равна

Следовательно,


Рис.5	Рис.6	Рис.7

Пример 11.

Определите электрическую энергию системы, состоящей из заряженного проводящего шара и концентрического с ним незаряженного проводящего шарового слоя (рис.6). Внутренний и внешний радиусы слоя a и b , радиус шара , заряд q , система находится в вакууме.

Одно из самых интересных и полезных открытий в механике —это закон сохранения энергии. Зная формулы для кинетической и потенциальной энергий механической системы, мы способны обнаруживать связь между состояниями системы в два разных момента времени, не вникая в подробности того, что происходит между этими моментами. Мы хотим определить теперь энергию электростатических систем. В электричестве сохранение энергии окажется столь же полезным для обнаружения многих любопытных фактов.

Закон, по которому меняется энергия при электростатическом взаимодействии, очень прост; на самом деле мы его уже обсуждали. Пусть имеются заряды q 1 и q 2 , разделенные промежутком r 12 . У этой системы есть какая-то энергия, потому что понадобилась какая-то работа, чтобы сблизить заряды. Мы подсчитывали работу, производимую при сближении двух зарядов с большого расстояния; она равна

Мы знаем из принципа наложения, что если зарядов много, то общая сила, действующая на любой из зарядов, равна сумме сил, действующих со стороны всех прочих зарядов. Отсюда следует, что полная энергия системы нескольких зарядов есть сумма членов, выражающих взаимодействие каждой пары зарядов по отдельности. Если q ¡ и q j — какие-то два из зарядов, а расстояние между ними r ij (фиг. 8.1), то энергия именно этой пары равна

Полная электростатическая энергия U есть сумма энергий всевозможных пар зарядов:

Если распределение задается плотностью заряда ρ, то сумму в (8.3) нужно, конечно, заменить интегралом.

Мы расскажем здесь об энергии с двух точек зрения. Первая — применение понятия энергии к электростатическим задачам; вторая — разные способы оценки величины энергии. Порой легче бывает подсчитать выполненную в каком-то случае работу, чем оценить величину суммы в (8.3) или величину соответствующего интеграла. Для образца подсчитаем энергию, необходимую для того, чтобы собрать из зарядов однородно заряженный шар. Энергия здесь есть не что иное, как работа, которая затрачивается на собирание зарядов из бесконечности.

Представьте, что мы сооружаем шар, наслаивая последовательно друг на друга сферические слои бесконечно малой толщины. На каждой стадии процесса мы собираем небольшое количество электричества и размещаем его тонким слоем от r до r + dr . Мы продолжаем процесс этот до тех пор, пока не доберемся до заданного радиуса а (фиг. 8.2). Если Q r — это заряд шара в тот момент, когда шар доведен до радиуса r, то работа, требуемая для доставки на шар заряда dQ , равна

Если плотность заряда внутри шара есть ρ, то заряд Q r равен

а заряд dQ равен

Электрический заряд – это физическая величина , характеризующая способность частиц или тел вступать в электромагнитные взаимодействия. Электрический заряд обычно обозначается буквами q или Q . В системе СИ электрический заряд измеряется в Кулонах (Кл). Свободный заряд в 1 Кл – это гигантская величина заряда, практически не встречающаяся в природе. Как правило, Вам придется иметь дело с микрокулонами (1 мкКл = 10 –6 Кл), нанокулонами (1 нКл = 10 –9 Кл) и пикокулонами (1 пКл = 10 –12 Кл). Электрический заряд обладает следующими свойствами:

Этот фактор называется электрическим точечным потенциалом . То есть: при электромагнетизме электрический потенциал или электростатический потенциал являются полем, эквивалентным потенциальной энергии , связанной со статическим электрическим полем, деленным на электрический заряд испытуемой частицы. Как хороший потенциал, только физические различия потенциалов имеют физическое значение. Электростатик является частью исследования электричества, которое изучает электрические заряды без движения, то есть в состоянии покоя.

Электростатическая и электродинамика

Электростатическое экранирование делает электрическое поле нулевым. Это связано с распределением избыточных электрических зарядов в проводнике. Нагрузки одного и того же сигнала имеют тенденцию уходить, пока они не достигнут покоя. В то время как электростатика изучает электрические заряды без движения, электродинамика изучает заряды в движении.

1. Электрический заряд является видом материи.

2. Электрический заряд не зависит от движения частицы и от ее скорости.

3. Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.

Таким образом, электростатика и электродинамика - это области изучения физики, которые посвящены различным аспектам электричества. В дополнение к этим областям также существует электромагнетизм, который изучает способность электричества привлекать и подавлять полюса.

После равновесия сфера А приводится в контакт с другой идентичной сферой С, которая имеет электрический заряд 3е. Какова будет плотность электрического заряда этого региона? Гидрофобный характер полиуретана связан с силой электростатического отталкивания между молекулами материала и молекулами воды, физическим явлением , которое происходит между телами с электрическими зарядами одного и того же сигнала. Правильно сказать, что сила электростатического отталкивания.

4. Существует два рода электрических зарядов, условно названных положительными и отрицательными .

5. Все заряды взаимодействуют друг с другом. При этом одноименные заряды отталкиваются, разноименные – притягиваются. Силы взаимодействия зарядов являются центральными, то есть лежат на прямой, соединяющей центры зарядов.

Это повод вернуться к приведенным выше примерам и спросить себя, почему весна прекращается достаточно быстро, чтобы колебаться, как и качели, если не поддерживать движение. Это потому, что есть трения, и они генерируют тепло, даже если мы этого не осознаем. Энергия очень постоянна, но часть рассеивается в виде тепла.

Материал, резервуар электрической и ядерной энергии

Однако, в отличие от массы, заряд может быть как положительным, так и отрицательным: сила тогда привлекательна, если заряды имеют противоположные знаки, но отталкивающие, если они имеют один и тот же знак. В электрической ячейке или другом генераторе электрические заряды с положительным знаком распределены на положительном полюсе, а электрические заряды с отрицательным знаком распределены на противоположном полюсе.

6. Существует минимально возможный (по модулю) электрический заряд, называемый элементарным зарядом . Его значение:

e = 1,602177·10 –19 Кл ≈ 1,6·10 –19 Кл.

Электрический заряд любого тела всегда кратен элементарному заряду:

где: N – целое число. Обратите внимание, невозможно существование заряда, равного 0,5е ; 1,7е ; 22,7е и так далее. Физические величины, которые могут принимать только дискретный (не непрерывный) ряд значений, называются квантованными . Элементарный заряд e является квантом (наименьшей порцией) электрического заряда.

В дополнение к своим проявлениям в электричестве это «кулоновское» взаимодействие отвечает за стабильность материи. Ядра положительного электрического заряда притягивают отрицательные электроны , что заставляет их образовывать атомы, которые сами притягивают друг друга. Более того, когда происходит химическая реакция, результатом является реорганизация ядер и электронов и модификация кулоновской энергии. Это называется химической энергией. Топливо, такое как уголь, бензин или водород, является резервуаром химической энергии , но эта энергия - не что иное, как кулоновская энергия.

В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:

Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. Из закона сохранения заряда так же следует, если два тела одного размера и формы, обладающие зарядами q 1 и q 2 (совершенно не важно какого знака заряды), привести в соприкосновение, а затем обратно развести, то заряд каждого из тел станет равным:

Эластичная энергия пружины, о которой мы говорили выше, также является следствием кулоновского взаимодействия. В ядерных ядрах имеются также ядерные взаимодействия, которые очень близки к ближнему и, следовательно, важны только внутри этих ядер. Они связывают нуклоны, т.е. протоны и нейтроны. Таким образом, можно выделять огромную энергию, комбинируя световые ядра. Огромную энергию также получают путем расщепления тяжелых ядер, таких как уран, который производится в бомбе А или в ядерном реакторе путем ядерного деления.

электрического поля

w = 1 2 ε 0 E2 + 1 2 E P. (11)

В формуле (11) первое слагаемое выражает плотность энергии электрического поля в вакууме, а второе слагаемое выражает энергию, затрачиваемую на поляризацию единицы объема диэлектрика.

В общем случае неоднородного электрического поля его энергию в некотором объеме V можно вычислить по формуле

4. Пондеромоторные силы. Применение закона сохранения энергии к расчету пондеромоторных сил.

На всякое заряженное тело, помещенное в электрическое поле, действуют механическая сила . Пондеромоторными называются силы, действующие со стороны электрического поля на макроскопические заряженные тела .

Определим силу взаимного притяжения между разноименно заряженными пластинами плоского конденсатора (пондеромоторную силу) двумя способами.

С одной стороны эту силу можно определить как силу F 2 , действующую на вторую пластину со стороны первой

F 2= Q 2E 1, (14)

где Q 2 – величина заряда на второй пластине,E 1 – напряженность поля первой пластины. Величина зарядаQ 2 второй пластины определяется формулой

Q 2 = σ 2 S , (15)

где σ 2 – поверхностная плотность заряда на второй пластине, а напряженностьЕ 1 поля, создаваемого первой пластиной вычисляется формулой

E 1 = σ 1 , (16)

где σ 1 – поверхностная плотность заряда на первой пластине. Подставим формулы (16) и (15) в формулу (14)

Учитывая, что σ = D = ε 0 ε E , получим формулу для силы, действующей на одну пластину со стороны другой

Для силы, действующей на единицу площади пластины, формула будет иметь следующий вид

F = ε 0 ε E 2 . (18)

Теперь получим формулу для пондеромоторной силы, используя закон сохранения энергии. Если тело перемещается в электрическом поле, то пондеромоторными силами

поля будет совершаться работа А. По закону сохранения энергии эта работа будет совершаться за счет энергии поля, то есть

A + W = 0 илиA = W . (19)

Работа по изменению расстояния между пластинами заряженного конденсатора на величину dx определяется формулой

где F – сила взаимодействия между обкладками (пондеромоторная сила).

Энергия заряженного конденсатора определяется формулой (9). При смещении одной из обкладок на расстояние dx энергии конденсатора изменится на величинуW

Как видим, формулы (18) и (22) одинаковые. Вместе с тем использование закона сохранения энергии для расчета пондеромоторных сил намного упрощает расчеты.

Вопросы для самопроверки:

1. Вывести формулу для энергии уединенного заряженного проводника и системы проводников.

2. Что является носителем электрической энергии? Что понимают под объемной

взаимодействия обкладок заряженного конденсатора?

Заряженный конденсатор обладает энергией. Проще всего выражение для этой энергии получить, рассматривая плоский конденсатор.

Энергия плоского конденсатора. Предположим, что пластины конденсатора, несущие равные и противоположные по знаку заряды, сначала расположены на расстоянии Затем одной из пластин мысленно дадим возможность перемещаться в направлении к другой пластине вплоть до полного их совмещения, коща заряды пластин компенсируются и конденсатор фактически исчезнет. При этом исчезает и энергия конденсатора, поэтому работа действующей на пластину электрической силы, совершаемая при ее перемещении, как раз и равна первоначальному запасу энергии конденсатора. Подсчитаем эту работу.

Сила, действующая на пластину, равна произведению ее заряда на напряженность однородного электрического поля, создаваемого другой пластиной. Эта напряженность, как мы видели в § 7, равна половине полной напряженности Е электрического поля внутри конденсатора, создаваемой зарядами обеих пластин. Поэтому искомая работа где - напряжение между

пластинами. Таким образом, выражение для энергии конденсатора через его заряд и напряжение имеет вид

Поскольку заряд конденсатора и напряжение связаны соотношением то формулу (1) можно переписать в эквивалентной форме так, чтобы энергия выражалась либо только через заряд либо только через напряжение

Энергия конденсатора. Эта формула справедлива для конденсатора любой формы. В этом можно убедиться, рассматривая работу, которую необходимо совершить для того, чтобы зарядить конденсатор, перенося заряд маленькими порциями с одной обкладки на другую. При вычислении этой работы следует учесть, что первая порция заряда переносится через нулевую разность потенциалов, последняя - через полную разность потенциалов а в каждый момент разность потенциалов пропорциональна уже перенесенному заряду.

Формулы (1) или (2) для энергии заряженного конденсатора можно, разумеется, получить как частный случай общей формулы (12) § 4, справедливой для энергии системы любых заряженных тел:

Энергию заряженного конденсатора можно трактовать не только как потенциальную энергию взаимодействия зарядов, но и как энергию создаваемого этими зарядами электрического поля, заключенного в пространстве между обкладками конденсатора. Обратимся опять для простоты к плоскому конденсатору, где электрическое поле однородно. Подставляя в выражение для энергии получаем

где - объем между обкладками конденсатора, заполненный электрическим полем.

Плотность энергии электрического поля. Энергия заряженного конденсатора оказывается пропорциональной занимаемому электрическим полем объему. Очевидно, что множитель, стоящий перед V в формуле (4), имеет смысл энергии, заключенной в единичном объеме, т. е. объемной плотности энергии электрического поля:

В СИ эта формула имеет вид

В системе единиц СГСЭ

Выражения для объемной плотности энергии справедливы при любой конфигурации электрического поля.

Энергия заряженного шара. Рассмотрим, например, энергию уединенного шара радиуса по поверхности которого равномерно распределен заряд . Такую систему можно рассматривать как предельный случай сферического конденсатора, радиус внешней обкладки которого стремится к бесконечности, а емкость принимает значение, равное радиусу шара (в системе единиц СГСЭ). Применяя для энергии формулу получаем

Если рассматривать эту энергию как энергию поля, создаваемого шаром, то можно считать, что вся она локализована в окружающем шар пространстве, а не внутри его, так как там напряженность поля Е равна нулю. Наибольшее значение объемная плотность имеет вблизи поверхности шара и очень быстро убывает при удалении от нее - как .

Собственная энергия точечного заряда. Таким образом, электростатическую энергию можно рассматривать либо как энергию взаимодействия зарядов, либо как энергию создаваемого этими зарядами поля.

Однако, рассматривая энергию двух разноименных точечных зарядов, мы приходим к противоречию. Согласно формуле (12) § 4 эта энергия отрицательна: а если ее рассматривать как энергию поля этих зарядов, то энергия получается положительной, так как плотность энергии поля, пропорциональная нигде не принимает отрицательных значений. В чем же здесь дело? Объясняется это тем, что в формуле (12) для энергии точечных зарядов учитывается лишь их взаимодействие, но не учитывается взаимодействие отдельных элементов каждого такого заряда между собой. Действительно, если мы имеем дело лишь с одним единственным точечным зарядом то энергия, вычисляемая по формуле (12), равна нулю, в то время как энергия электрического поля этого заряда имеет положительное (бесконечное для истинно точечного заряда) значение, равное так называемой собственной энергии заряда .

Чтобы убедиться в этом, обратимся к формуле (8) для энергии заряженного шара. Если устремить в ней к нулю, то мы и придем к точечному заряду. С уменьшением плотность энергии растет настолько быстро, что, как видно из (8), полная энергия поля оказывается бесконечно большой. В классической электродинамике собственная энергия точечного заряда бесконечна.

Собственная энергия произвольного заряда может рассматриваться как энергия взаимодействия его частей. Эта энергия зависит, конечно, от размеров и формы заряда. Часть ее освободилась бы при «взрыве» и разлете «осколков» заряда под действием кулоновских сил отталкивания, превратившись в кинетическую энергию «осколков», другая ее часть осталась бы в форме собственной энергии этих «осколков».

Рассмотрим теперь полную, т. е. собственную и взаимную, энергию двух зарядов Пусть каждый из этих зарядов в отдельности создает соответственно поле так что результирующее поле Объемная плотность энергии поля распадается на три слагаемых в соответствии с выражением

Первые два слагаемых в правой части соответствуют объемной плотности собственных энергий зарядов а третье слагаемое соответствует энергии взаимодействия зарядов друг с другом. Именно эта часть полной энергии системы и дается формулой (12) § 4. Из очевидного неравенства следует, что Таким образом, положительная собственная энергия зарядов всегда больше или в крайнем случае равна их взаимной энергии. Насмотря на то, что взаимная энергия может принимать как положительные, так и отрицательные значения, полная энергия, пропорциональная всегда положительна.

При всех возможных перемещениях зарядов, не изменяющих их формы и размеров, собственная энергия зарядов остается постоянной. Поэтому при таких перемещениях изменение полной энергии системы зарядов равно изменению их взаимной энергии. Так как во всех физических явлениях существенно именно изменение энергии системы, то постоянная часть - собственная энергия зарядов - может быть отброшена. В этом смысле и следует понимать утверждение об эквивалентности энергии взаимодействия зарядов и энергии создаваемого ими поля. Итак, мы можем сопоставлять системе зарядов либо полную энергию - энергию поля, либо энергию взаимодействия и будем получать при этом, вообще говоря, разные значения. Но, рассматривая переход системы из одного состояния в другое, мы для изменения энергии всегда получим одну и ту же величину.

Обратим внимание, что при использовании формулы (12) § 4 для системы точечных зарядов и проводников мы получаем, как видно

из самого вывода формулы, собственную энергию проводников и взаимную потенциальную энергию всех входящих в систему зарядов, т. е. полную энергию поля за вычетом неизменной собственной энергии точечных зарядов.

Собственная энергия проводника. Собственная энергия проводников, в отличие от собственной энергии точечных зарядов, не является постоянной. Она может измениться при изменении конфигурации системы вследствие перемещения зарядов в проводниках. Поэтому эта энергия не может быть отброшена при вычислении изменения энергии системы.

В том случае, когда система состоит только из проводников, а точечных зарядов нет, формула (12) §4 дает полную энергию системы, т. е. сумму собственных энергий всех проводников и энергии их взаимодействия. Мы получаем одно и то же значение независимо от того, рассматриваем ли энергию поля или энергию системы зарядов. Примером такой системы является конденсатор, где, как мы видели, оба подхода дают одинаковый результат

Очевидно, что при наличии точечных зарядов и проводников не имеет смысла рассматривать по отдельности собственную энергию проводников и взаимную потенциальную энергию всех зарядов, так как работа внешних сил определяет изменение суммы этих энергий. Исключить из рассмотрения можно только неизменную собственную энергию точечных зарядов.

Энергетические превращения в конденсаторах. Для анализа энергетических превращений, которые могут происходить в электрическом поле, рассмотрим плоский конденсатор с воздушным зазором, подсоединенный к источнику с постоянным напряжением Будем раздвигать пластины конденсатора от расстояния до расстояния в двух случаях: предварительно отсоединив конденсатор от источника питания и не отсоединяя конденсатор от источника.

В первом случае заряд на обкладках конденсатора все время остается неизменным: хотя емкость С и напряжение изменяются при движении пластин. Зная напряжение на конденсаторе в начальный момент, находим величину этого заряда (в единицах СИ):

Так как разноименно заряженные пластины конденсатора притягиваются, для их раздвижения необходимо совершить положительную механическую работу. Если при раздвижении расстояние между пластинами все время остается много меньше их линейных размеров, то сила притяжения пластин не зависит от расстояния между ними.

Для равномерного перемещения пластины внешняя сила должна уравновесить силу притяжения, и поэтому совершаемая при перемещении пластины на расстояние механическая работа равна

так как где - неизменная напряженность поля, создаваемого зарядами обеих обкладок. Подставляя в (11) заряд из (10) и находим

Второй случай отличается от рассмотренного тем, что при движении пластин остается неизменным не заряд конденсатора, а напряжение на нем: Поскольку расстояние между обкладками увеличивается, то напряженность поля убывает, а следовательно, убывает и заряд на пластинах. Поэтому сила притяжения пластин не остается постоянной, как в первом случае, а убывает, причем, как нетрудно убедиться, обратно пропорционально квадрату расстояния. Вычислить работу этой переменной силы можно с помощью закона сохранения и превращения энергии.

Применим его сначала к более простому первому случаю. Изменение энергии конденсатора происходит только за счет механической работы, совершаемой внешними силами: Поскольку заряд конденсатора остается неизменным, для энергии конденсатора удобно воспользоваться формулой Таким образом,

что при подстановке выражения для емкости и для заряда (10) приводит к окончательной формуле (12). Обратим внимание, что этот результат можно получить и рассматривая энергию конденсатора как энергию электрического поля между его обкладками. Так как напряженность поля и, следовательно, плотность энергии остаются неизменными, а объем, занимаемый полем, возрастает, то увеличение энергии равно произведению плотности энергии на приращение объема

Во втором случае энергия конденсатора изменяется как за счет механической работы, так и за счет работы, совершаемой источником питания:

Определив независимо изменение энергии конденсатора и работу источника, можно с помощью закона сохранения энергии (13) найти механическую работу.

Поскольку в этом случае остается неизменным напряжение, для расчета энергии конденсатора удобно использовать формулу Для изменения энергии получаем

При изменении заряда на обкладках конденсатора на величину источник питания совершает работу Заряд конденсатора определяется соотношением Тогда

и с помощью выражения (13) получаем

Отметим, что из (15) и (14) видно, что

т. е. работа источника равна удвоенному изменению энергии конденсатора.

Интересно отметить, что как работа источника, так и изменение энергии конденсатора получились отрицательными. Это вполне понятно: совершаемая механическая работа положительна и должна была бы привести к увеличению энергии конденсатора (как и происходит в первом случае). Но энергия конденсатора убывает, и, следовательно, источник должен «принять на себя» энергию, равную убыли энергии конденсатора и механической работе внешних сил. Если процессы в источнике обратимы (аккумулятор), то он будет заряжаться, в противном случае источник просто нагревается.

Чтобы лучше разобраться в сути явлений, рассмотрим противоположный случай: присоединенные к источнику пластины конденсатора сближают от расстояния до расстояния Поскольку пластины притягиваются, работа внешних сил отрицательна, ибо для равномерного перемещения пластин внешняя сила должна быть направлена в сторону, противоположную перемещению. Энергия конденсатора при сближении пластин возрастает. Итак, механическая работа внешних сил отрицательна, а энергия конденсатора возросла, следовательно, источник совершил положительную работу. Половина этой работы равна увеличению энергии конденсатора, вторая половина передана внешним телам в виде механической работы при сближении пластин. Все приведенные выше формулы применимы, разумеется, при любом направлении перемещения пластин.

Во всех рассуждениях мы пренебрегали сопротивлением проводов, соединяющих конденсатор с источником. Если учитывать выделяющуюся в проводах при движении зарядов теплоту уравнение

баланса энергии принимает вид

Изменение энергии конденсатора и работа источника выражаются, конечно, прежними формулами (14) и (15). Теплота всегда выделяется независимо от того, сближаются или раздвигаются пластины, поэтому Значение можно вычислить, если известна скорость движения пластин. Чем больше скорость движения, тем больше выделяющаяся теплота. При бесконечно медленном движении пластин

Изменение энергии и работа источника. Выше мы отметили, что работа источника питания при раздвижении пластин равна удвоенному изменению энергии конденсатора. Этот факт носит универсальный характер: если любым способом изменить энергию подсоединенного к источнику питания конденсатора, то работа, совершаемая при этом источником питания, равна удвоенному значению изменения энергии конденсатора:

Как в этом убедиться? Поскольку конденсатор все время остается присоединенным к источнику питания, напряжение на конденсаторе равно как в начале, так и в конце процесса (хотя во время процесса напряжение на конденсаторе может быть и меньше). Если заряд конденсатора во время процесса изменился на величину то его энергия изменилась на величину

При этом источник питания совершил работу

Чтобы не возникало подозрений в том, что половина энергии «бесследно исчезла», напишем уравнение баланса энергии:

где - механическая работа, совершенная при этом процессе силами, действующими на внешние тела, выделившаяся теплота. Очевидно, что и равно оставшейся половине работы источника. Существуют такие процессы, в которых либо либо Но, как видно из (16) и (17), изменение энергии конденсатора, соединенного с источником, обязательно сопровождается либо совершением механической работы, либо выделением теплоты.

Получите формулу для энергии заряженного конденсатора, рассматривая работу, совершаемую при его зарядке путем переноса заряда с одной обкладки на другую.

Поясните качественно, почему объемная плотность энергии электрического поля пропорциональна квадрату его напряженности.

Что такое собственная энергия точечного заряда? Как в электростатике преодолевается трудность, связанная с бесконечным значением собственной энергии точечных зарядов?

Поясните, почему два первых слагаемых в правой части формулы (9) соответствуют объемной плотности собственных энергий точечных зарядов а третье слагаемое - энергии взаимодействия зарядов друг с другом.

Как связаны между собой изменение энергии конденсатора при каком-либо процессе и работа источника питания, к которому подсоединен этот конденсатор в течение всего процесса?

При каких условиях изменение энергии конденсатора, соединенного с источником питания, не сопровождается выделением теплоты?

Конденсатор с диэлектриком. Рассмотрим теперь энергетические превращения в конденсаторах при наличии диэлектрика между обкладками, считая для простоты его диэлектрическую проницаемость постоянной. Емкость конденсатора с диэлектриком в раз больше, чем емкость С такого же конденсатора без диэлектрика. Конденсатор с зарядом отсоединенный от источника питания, обладает энергией

Рис. 52. Втягивание пластины из диэлектрика в плоский конденсатор

При заполнении пространства между обкладками диэлектриком с проницаемостью энергия конденсатора уменьшится в раз: Отсюда сразу можно сделать вывод о том, что диэлектрик втягивается в электрическое поле.

Втягивающая сила при неизменном заряде конденсатора убывает по мере заполнения диэлектриком пространства между обкладками. Если на пластинах конденсатора поддерживается постоянное напряжение, то сила, втягивающая диэлектрик, не зависит от длины втянутой части.

Для нахождения силы, действующей на диэлектрик со стороны электрического поля, рассмотрим втягивание твердого диэлектрика в горизонтально расположенный конденсатор, соединенный с источником постоянного напряжения (рис. 52). Пусть под действием интересующей нас втягивающей силы и какой-то внешней силы кусок диэлектрика находится в Для нахождения высоты подъема жидкого диэлектрика приравняем вычисленную втягивающую силу весу поднявшейся жидкости и получим

Для нахождения выделившейся при подъеме жидкости теплоты проще всего исходить из закона сохранения энергии. Поскольку поднятый столб жидкости покоится, совершенная источником работа равна сумме изменений энергий конденсатора и потенциальной энергии диэлектрика в поле тяжести, а также выделившейся теплоты

Учитывая, что и пользуясь соотношением (21), находим

Таким образом, работа источника питания разделилась пополам: одна половина пошла на увеличение электростатической энергии конденсатора; вторая половина разделилась поровну между увеличением потенциальной энергии диэлектрика в поле тяжести и выделившейся теплотой. Как происходило выделение этой теплоты? При погружении пластин конденсатора в диэлектрик жидкость начинает подниматься, приобретая кинетическую энергию, и по инерции проскакивает положение равновесия. Возникают колебания, которые постепенно затухают из-за вязкости жидкости, и кинетическая энергия превращается в теплоту. Если вязкость достаточно велика, то колебаний может и не быть - вся теплота выделяется при подъеме жидкости до положения равновесия.

Сформулируйте закон сохранения энергии для процесса, в котором наряду с изменением электростатической энергии изменяется еще какая-либо энергия и происходит выделение теплоты.

Поясните физический механизм возникновения сил, втягивающих диэлектрик в пространство между пластинами заряженного конденсатора.

7. Энергия электрического поля

(Примеры решения задач)

Энергия взаимодействия зарядов

Пример 1.

Определите электрическую энергию взаимодействия точечных зарядов, расположенных в вершинах квадрата со стороной a (см. рис.2).

Решение .

На рис.3 условно изображены двунаправленными стрелками все парные взаимодействия зарядов. Учитывая энергии всех этих взаимодействий, получим:

Пример 2.

Решение .

При решении задачи следует учесть все энергии парных взаимодействий зарядов одного тела (кольца) с зарядами другого тела (диполя). Энергия взаимодействия точечного заряда q с зарядомQ , распределенным по кольцу, определяется суммой

где
- заряд бесконечно малого фрагмента кольца, - расстояние от этого фрагмента до зарядаq . Поскольку всеодинаковы и равны
, то

Аналогично найдем энергию взаимодействия точечного заряда –q с заряженным кольцом:

Суммируя W 1 иW 2 , получим для энергии взаимодействия кольца с диполем:

Электрическая энергия заряженных проводников

Пример 3.

Решение .

Электрическая энергия уединенного проводника определяется формулой
, гдеq – заряд проводника,- его потенциал. Учитывая, что потенциал однородно заряженной сферы радиусаR равен
, найдем ее электрическую энергию:

После уменьшения в два раза радиуса сферы ее энергия становится равной

Электрические силы при этом совершают работу

Пример 4.

Решение .

После соединения шаров тонкой проволокой их потенциалы становятся одинаковыми

Из этих уравнений найдем

,
.

Энергия шаров до соединения их проволокой равна

а после соединения

Подставляя в последнее выражение значения Q 1 и Q 2 , получим после простых преобразований

Пример 5.

Решение .

При слиянии ртутных шариков сохраняется их суммарный заряд и объем:

Электрическая энергия полученного в результате слияния шара

После алгебраических преобразований получим

= 4.

Пример 6.

Металлический шарик радиуса R = 1 мм и заряда q = 0,1 нКл с большого расстояния медленно приближают к незаряженному проводнику и останавливают, когда потенциал шарика становится равным  = 450 В. Какую работу для этого следует совершить?

Решение .

где q 1 иq 2 – заряды проводников, 1 и 2 – их потенциалы. Так как проводник по условию задачи не заряжен, то

где q 1 и 1 заряд и потенциал шара. Когда шар и незаряженный проводник находятся на большом расстоянии друг от друга,

и электрическая энергия системы

В конечном состоянии системы, когда потенциал шара стал равным , электрическая энергия системы:

Работа внешних сил равна приращению электрической энергии:

= –0,0225 мкДж.

Пример 7 .

Система состоит из двух концентрических тонких металлических оболочек с радиусами R 1 и R 2 (
и соответствующими зарядамиq 1 и q 2 . Найдите электрическую энергию W системы. Рассмотрите также специальный случай, когда
.

Решение .

Электрическая энергия системы из двух заряженных проводников определяется формулой

Для решения задачи необходимо найти потенциалы внутренней ( 1) и внешней ( 2) сфер. Это нетрудно сделать (см. соответствующий раздел пособия):

,
.

Подставляя эти выражения в формулу для энергии, получим

При
энергия равна

Собственная электрическая энергия и энергия взаимодействия

Пример 8.

Решение .

Электрическая энергия двух удаленных друг от друга заряженных сфер равна

Электрическая энергия полученного сферического конденсатора:

Потенциал внутренней сферы,
- потенциал внешней сферы. Следовательно,

Работа электрических сил при таком составлении конденсатора:

Заметим, что электрическая энергия сферического конденсатора W 2 равна работе внешних сил по зарядке конденсатора. При этом электрические силы совершают работу
. Эта работа совершается не только при сближении заряженных обкладок, но и при нанесении заряда на каждую из обкладок. ПоэтомуA ЭЛ отличается от найденной выше работы A , совершенной электрическими силами только при сближения обкладок.

Пример 9.

Решение .

Энергия взаимодействия точечного заряда q с зарядами, расположенными на сферической оболочке радиуса R равна

Собственная электрическая энергия оболочки (энергия взаимодействия зарядов оболочки между собой) равна:

Работа электрических сил при расширении оболочки:

После преобразований получим

1,8 Дж.

Другой способ решения

Потенциал сферы радиуса r ,

Потенциал сферы радиуса R . При расширении внешней сферы электрические силы совершают работу

После подстановок и преобразований получим ответ.

Объемная плотность энергии электрического поля

Пример 10 .

Решение .

Объемная плотность энергии электрического поля

определяет электрическую энергию
, локализованную в бесконечно малом объеме
(E – модуль вектора напряженности электрического поля в этом объеме,  - диэлектрическая проницаемость). Чтобы вычислить полную электрическую энергию заряженного проводящего шара, мысленно разобьем все пространство на бесконечно тонкие шаровые слои, концентрические с заряженным шаром. Рассмотрим один из таких слоев радиуса r и толщины dr (см. рис.5). Его объем равен

а сосредоточенная в слое электрическая энергия

Напряженность E поля заряженного проводящего шара зависит, как известно, от расстояния r до центра шара. Внутри шара
, поэтому при вычислении энергии достаточно рассматривать только те шаровые слои, радиусr которых превышает радиус шара R .

При
напряженность поля

диэлектрическая проницаемость
и, следовательно

где q – заряд шара.

Полная электрическая энергия заряженного шара, определяется интегралом

а энергия, сосредоточенная внутри воображаемой сферы радиуса nR , равна

Следовательно,

Пример 11.

Определите электрическую энергию системы, состоящей из заряженного проводящего шара и концентрического с ним незаряженного проводящего шарового слоя (рис.6). Внутренний и внешний радиусы слоя a и b , радиус шара
, зарядq , система находится в вакууме.

Решение .

На внутренней и внешней поверхностях шарового слоя распределены индуцированные заряды. Их алгебраическая сумма равна нулю, поэтому индуцированные заряды не создают электрического поля при
, гдеr – расстояние от центра системы. В области
напряженность поля индуцированных зарядов также равна нулю, поскольку они однородно распределены по сферическим поверхностям. Таким образом, электрическое поле системы совпадает с полем однородно заряженной по поверхности сферы, за исключением внутренней области шарового слоя, гдеE = 0. На рис.7 приведен примерный график зависимости
. Опуская подробные выкладки (см. пример 10), запишем для электрической энергии системы:

где
,
,
. После интегрирования получим

Пример 12.

Первоначально заряд q распределен однородно по объему шара радиуса R . Затем вследствие взаимного отталкивания заряды переходят на поверхность шара. Какую работу совершают при этом электрические силы? Диэлектрическую проницаемость считайте равной единице.

Решение .

Работа электрических сил равна убыли электрической энергии:

где W 1 – электрическая энергия однородно заряженного по объему шара,W 2 – энергия того же шара, однородно заряженного по поверхности. Поскольку суммарный заряд в обоих случаях одинаков, то электрическое поле вне шара при переходе заряда из объема на поверхность не изменяется. Электрическое поле и энергия изменяются только внутри шара.

При помощи теоремы Гаусса можно вывести формулу для напряженности поля внутри однородно заряженного шара на расстоянии r от его центра:

Электрическая энергия, сосредоточенная внутри шара, определяется интегралом:

Когда все заряды перешли на поверхность шара, электрическое поле, а следовательно, и энергия электрического поля внутри шара стали равными нулю. Таким образом,